Our Research

• Learning, adaptation and optimization are our main research fields. Although there can be many approaches to these fields, we employ a statistical approach having the sound theoretical grounds and a wide variety of applications. At the same time we employ a numerical approach to avoid combinatorial explosion inevitably arising in a combinatorial approach.

• With these in mind, we aim to achieve two research goals: invention of innovative learning algorithms of machine learning, and addressing challenging applications of machine learning. As for the first, we strive to invent smart learning algorithms for such learning models as neural networks, EM algorithm, kernel machines, genetic algorithms, and classifier systems. As for the second, we consider various kinds of discovery of intrinsic hidden structures from several kinds of data, and job shop scheduling using genetic algorithms. Through addressing these challenging applications, we invent and polish learning algorithms necessary to solve given problems.

• Our research topics are shown below. Our research results have got more than 6,000 citations according to GoogleScholar.

As for inventing innovative learning algorithms, we've had the following activities.

• 2nd-order Learning for Multi-Layer Perceptrons (MLPs):
  

  BPQ (BP based on Partial Quasi-Newton) [J13], invented for MLP learning by us, has been our precious method working nicely in so many situations. For our all cases, BPQ worked far faster and got much better solutions than BP. In BPQ, search direction is calculated using BFGS update, and step length is calculated using 2nd-order approximation.

• Neural Networks Learning using Singular Regions:
  

  Most learning models are singular. A singular model has flat search areas called singular regions; any gradient-based search is easily trapped there and cannot move, well-known stagnation of learning. Recently we have invented two epochal methods: SSF (singularity stairs following) [J49] for MLPs, and RBF-SSF [C104, 105] for radial basis function networks. SSF and RBF-SSF make good use of singular regions as starting points to find systematically a series of excellent solutions. We expect they can find the best solutions for any given data.

  
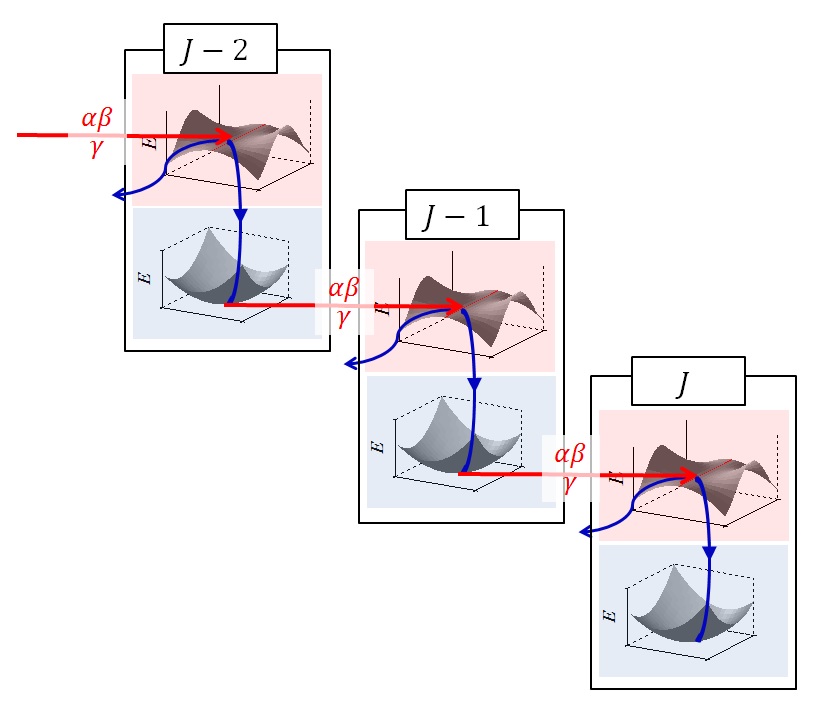
  search behavior of SSF: SSF goes down Singularity Stairs.

• Advanced MLP Models Learning:
  

  We investigated two advanced MLP models and the corresponding learning methods. One is a complex-valued MLP (C-MLP). C-MLP has the attractive potential real-valued MLP doesn't have. Empolying Wirtinger calculus to calculate the gradient and Hessian of C-MLP, we've invented C-SSF (complex-valued SSF) [C95, C99] for C-MLPs. The performance of C-SSF far outperformed the existing methods. The other is an MLP with common weights, which work for avoiding over-fitting. Learning of this model is really hard, but we finally invented BCW (bidirectional clustering of weights) [C56], which worked nicely, finding satisfactory common weights.

  
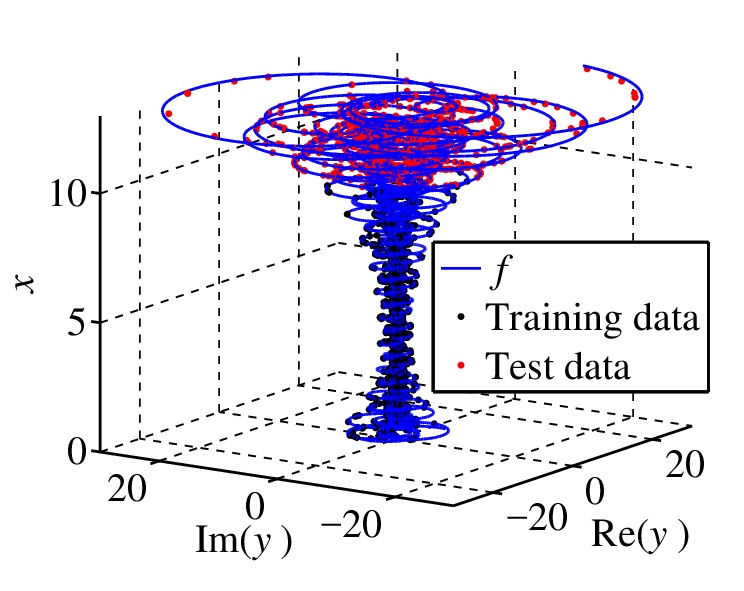
  complicated spiral learned by C-SSF for C-MLP.

• Variants of the EM Algorithm:
  

  The EM algorithm is a very efficient algorithm to obtain maximum likelihood estimate for incomplete data, but has the local optimality problem. Toward global optimality, we investigated several EM extensions; for example, by introducing the deterministic annealing (DA) framework, we had DAEM algorithm [J22], or by repeating expanding or shrinking of model size using split-merge operations, we had SMEM algorithm [C44, J31]. On this topic we've got more than 1,200 citations according to GoogleScholar.

• Support Vector Regression (SVR):
  

  We investigate support vector regression which shows excellent generalization. Since SVR hyperparameters have considerable influence on the generalization performance, we invented SVR/MCV [C57, C69] to find the optimal set of hyperparameters using the MCV (minimum cross validation) framework.

As for addressing challenging applications of machine learning, we've had the following activities. The first four can be consindered as discovery of hidden structures from data.

• Numeric Law Discovery using Neural Networks:
  

  Discovering understandable numeric relations such as polynomials from data is one of the key issues of data mining. We invented a couple of methods each of which performs multivariate polynomial regression using MLP and BPQ. First, we invented RF5 (rule extraction from facts, ver. 5) [C32, C34] which discovers the adequate polynomial from numeric data. As one example, RF5 discovered Kepler's third law. Next, we investigated extracting laws from data including numeric and nominal variables. And we invented RF6 [C47] which learns the whole data using a single MLP and then decomposes into a set of rules, where a rule means a nominally conditioned polynomial. RF6 was applied to real data to find interesting results. Finally, we invented RN2 (rule extraction from neural nets, ver. 2) [J37], which extracts regression rules from trained neural networks. RN2 uses VQ (vector quantizer) and decision trees for rule extraction. RN2 found interesting regression rules from financial or automobile data sets.

  
  numerical law (multivariate polynomials) discovery by neural networks.

• Behavioral Rules Learning using Classifier Systems:
  

  Thrown into an unknown environment, an intelligent agent acts by trial and error and gradually learns behavioral rules through experiences. For this learning we adopt a learning classifier system (LCS) framework as a brain of the agent. Although LCS usually uses GA, we introduced new neural learning called bidirectional competitive learning and built NCS (neural classifier system) [C50]. NCS can find behavioral rules through experiences; for example, could solve quite hard 70-multiplexer problem completely after 10 million cycles. We believe NCS has the good potential.

  
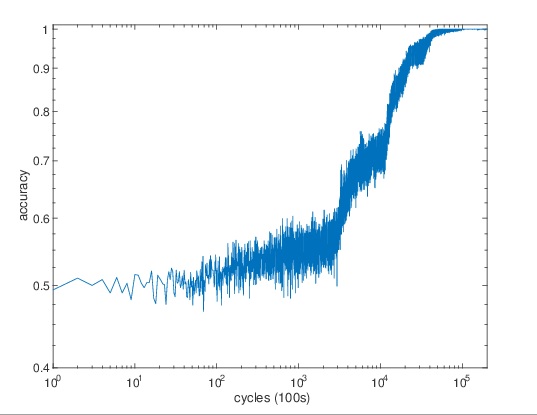
  NCS completely learns 70-MPX problem after ten million cycles.

• L-system Grammar Induction:
  

  The induction of L-system grammar is an open problem little explored so far. We have invented two learning algorithms. LGIN (L-system Grammar Induction based on Number theory) [C88] can find the original grammar from a noiseless sentence of thousands of characters within one second. LGIC2 (L-system Grammar Induction with error Correction, ver. 2) [C93] can find the original grammar using emergent induction from a noisy sentence of thausands of characters within minites or 30 minites depending on noise level.

  
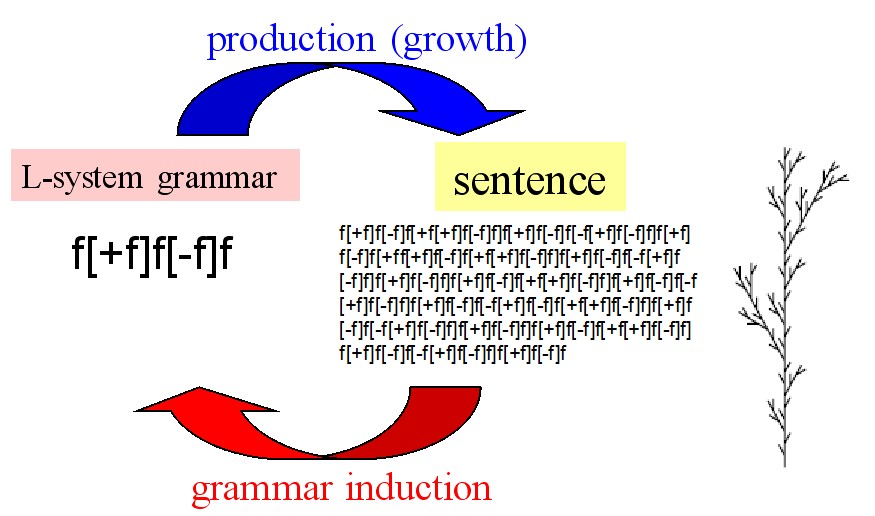
  L-system grammar induction.

  
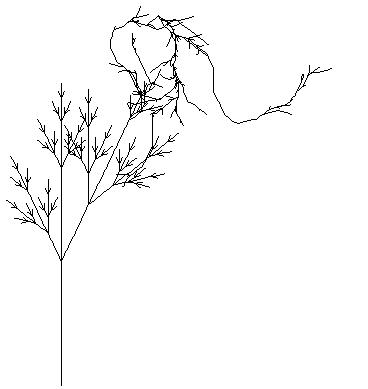
  LGIC2 can find the original grammar from a sentence having rather heavy transmutation like this.

• Social Network Analysis:
  

  Global human activities through the Internet have evolved to form complex networks called social networks. We investigate methods [C73, J45] which extract influential nodes in social networks using machine learning frameworks.

• Job Shop Scheduling using Genetic Algorithms:
  

  We got interested in the evolutionary framework, and wanted to develop excellent algorithms using genetic algorithm (GA) to solve job shop scheduling problems (JSSPs) known as hard combinatorial problems. We invented many smart algorithms. First, we invented forcing GA [C05] by introducing forcing into GA, where forcing means replacing illegal genotype with the closest legal one. Forcing GA showed for the first time in the world that GA can solve rather hard JSSPs. Next, we invented GA/GT [C07] using Giffler & Thompson (GT) representation, which could solve larger scale of JSSPs. Then, we introduced MSXF (multi-step crossover and local search) to have GA/MSXF [C28], which stably showed the best performance at that time. Finally, we invented CBSA+SB [C17] by enhancing CBSA (critical block simulated annealing) with SB (shifting bottleneck). CBSA+SB showed the best performance for ten tough JSSPs. On this topic we've got more than 1,800 citations according to GoogleScholar.

  
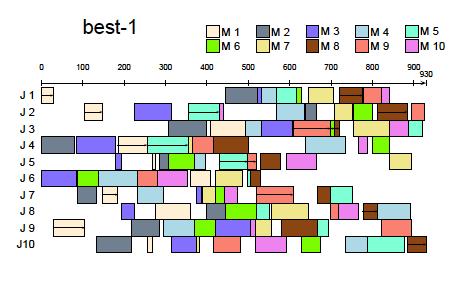
  an optimal schedule for mt10x10 problem obtained by GA/GT.

Back to Ryohei Nakano's Top Page